例題1: 1次元拡散方程式

問題の説明とシリアルFortranプログラム

周期的な領域 $x\in \left[-1,1\right]$ において， $f\left(x,t\right)$ に対する1次元拡散方程式

$\frac{\partial f}{\partial t}=D\frac{{\partial }^{2}f}{\partial x^2}$

を考えます． $D$は拡散係数．有限差分法を用いて以下のように近似します．

$\frac{f_i^{n+1}-f_i^n}{\mathrm{\Delta t}}=D\frac{f_{i+1}^n-2f_i^n+f_{i-1}^n}{{\left(\mathrm{\Delta x}\right)}^2}$.

$\mathrm{\Delta t}$は時間刻み幅，$\mathrm{\Delta x}$は空間格子の刻み幅です．時間，空間はそれぞれ $t_n=n\mathrm{\Delta t}+t_0,x_i=i\mathrm{\Delta x}+x_0$ と離散化されます．ここで $t_0$， $x_0$ は起点を表しますが，後の議論に関係しませんので特に気にする必要はありません． $f_i^n$ は $n$ステップ目の時刻の，$i$番目の格子点における$f$の値を表します． $f_i^{n+1}$ について解くと

$f_i^{n+1}=f_i^n+\frac{D\mathrm{\Delta t}}{{\left(\mathrm{\Delta x}\right)}^2}\left(f_{i+1}^n,-,2,f_i^n,+,f_{i-1}^n\right)$

が得られます．これは時間ステップ$n$における$f$の値を用いて，次の時間ステップ$n+1$における$f$の値が計算できることを表しています．この1次元拡散方程式の有限差分解を求めるプログラムをFortran90によって作成したものが以下です． （以下にサンプルソースコードが表示されない場合はこちらのサンプルコードを参照してください．）

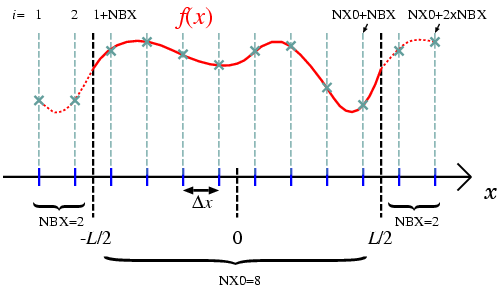
図1にプログラム中における空間格子の配置を示します．領域の大きさは$L$でプログラム中でLENGTHで与えられ，座標の起点は $x_0=-L/2-\mathrm{\Delta x}/2$ となります．領域内，外の格子点数はそれぞれNX0，NBXで与えられ，全格子点数はnx=NX0+2*NBXとなります．領域外の格子点は，境界での値を計算するために必要になります．例えば，領域内左端の格子（1+NBX）の値を計算するには，両隣（NBXと2+NBX）での値が必要になります．この場合NBXは1で十分ですが，高次の差分では領域外に1つ以上の格子点が必要になる場合がありますので，図1ではより一般的な場合を示しています．ここで示したような格子点配置では，周期境界条件は（1:NBX）の格子点のデータを（NX0+1:NX0+NBX）と同一視し，（NX0+NBX+1:NX0+NBX+NBX）の格子点のデータを（NBX+1:NBX+NBX）の格子点のデータと同一視することで満たされます．

プログラム中，全質量

$F={\int }_{-L/2}^{L/2}f\text{d}x$

も計算されていますが，これは周期境界条件下では保存量であり，時間的に変化しません．保存量$F$が正しく保存しているかどうかは，数値解が正しいかどうかのひとつの目安となります．以下はこのプログラムの標準出力です．

	    ./diffuse_serial < diffuse.param.in
time =       0.0000, total =       1.0000, difference =       0.0000 [%]
time =       0.1221, total =       1.0000, difference =      -0.0000 [%]
time =       0.2441, total =       1.0000, difference =       0.0000 [%]
time =       0.3662, total =       1.0000, difference =      -0.0000 [%]
time =       0.4883, total =       1.0000, difference =      -0.0000 [%]
time =       0.6104, total =       1.0000, difference =      -0.0001 [%]
	  

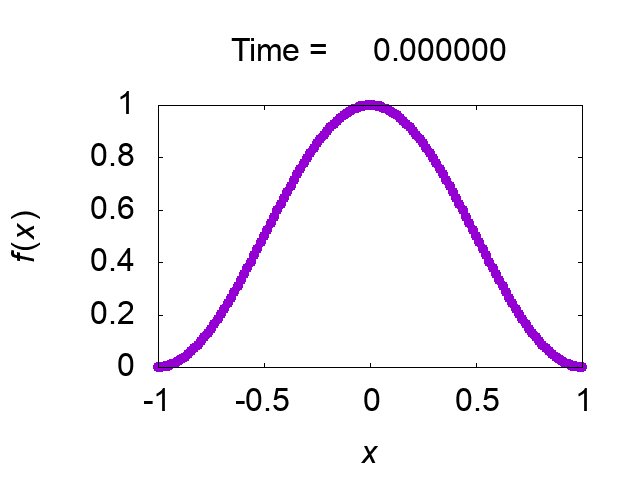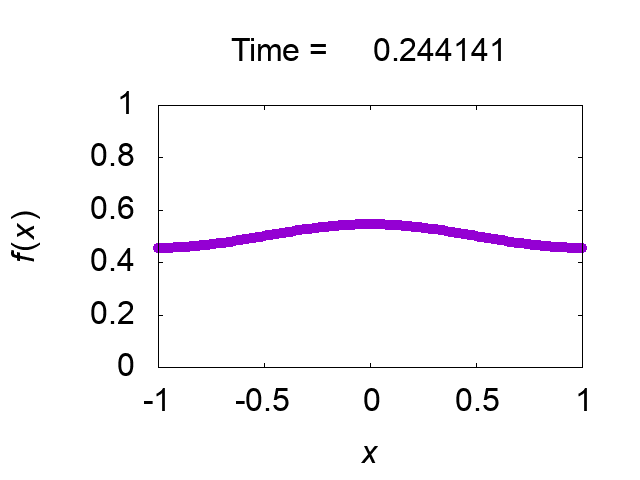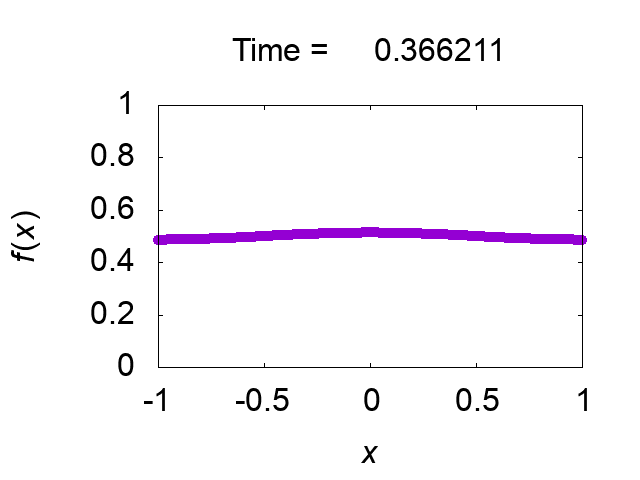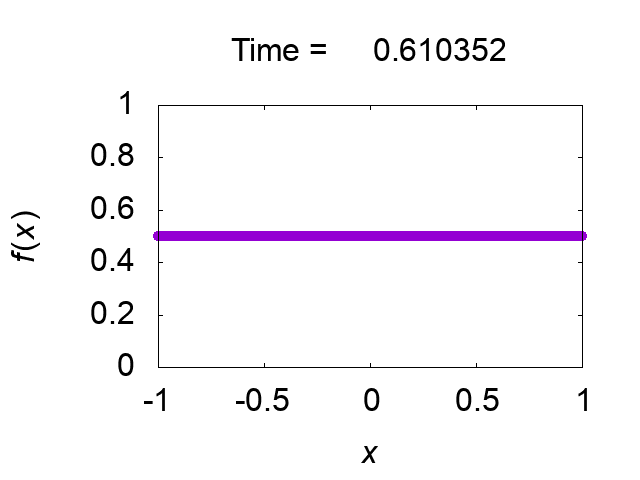
"difference [%]"は保存量の初期値との差異を出力していますが，解は正しく求められているようです．図2に解の時間発展を示します．

並列化

並列化とはプログラム中の互いに依存しない処理を異なるプロセッサ上に分散配置し，複数のプロセッサで同時に計算させることで，理想的には実行時間を1/(プロセッサ数)に減らすことができます（実際は，プロセッサ間のデータの通信，非均等な処理の分散，並列化できない処理の存在などにより，理想的な並列化は不可能ですが）．ここで考えている問題においては，$f$を求める計算は，両隣の格子点における$f$の値しか必要としないため並列化可能です．そこで，$f$をいくつかのプロセッサに分散することを考えてみましょう．$N_{\text{p}}$をプロセッサ数，$N_x$を領域内の格子点数とします．$I_{\text{p}}$番目（ $I_{\text{p}}=0,\cdots ,N_{\text{p}}-1$ ）のプロセッサは，以下で与えられる$N_{\text{min}}$から$N_{max}$までの格子点における計算を受け持ちます．（ただし，この分割方法では$N_{\text{p}}$が大きい時仕事量が均等ではなくなります．）

$\begin{array}{ccc}{N}_{\text{min}}& =& \text{int}\left(\frac{N_x}{N_{\text{p}}}\right)I_{\text{p}}+1\\ N_{\text{max}}& =& \text{max}\left(\text{int}\left(\frac{N_x}{N_{\text{p}}}\right)\left(I_{\text{p}}+1\right),N_x\right)\end{array}$

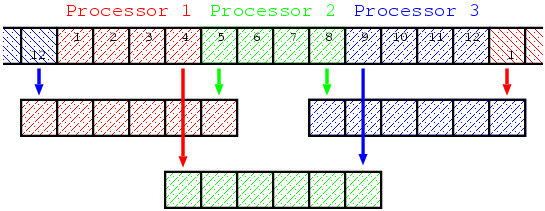
ここで $\text{max}\left(a,b\right)$ は$a$, $b$のうち大きい方を返す関数， $\text{int}\left(a\right)$ は小数点以下を切り捨てた$a$の整数部を返す関数とします．次の図は，データがどのように分散されるかを示しています．

$f_i^{n+1}$ を計算するためには，両隣の格子点での値 $f_{i+1}^n$ と $f_{i-1}^n$ が必要になりますが，各プロセッサは受け持っている格子点の両端の格子点での値を計算するために必要なデータを持っていません．例えば $N_x=12$, $N_{\text{p}}=3$ としましょう．1番目のプロセッサは1番目から4番目の格子を受け持ちますが，4番目の格子点の$f$を計算するために必要な5番目の格子のデータは持っていません．周期境界条件では，1番目のプロセッサは格子1の$f$を計算するために必要な格子0と同一視される格子12のデータも持っていないことになります．同様にしてプロセッサ2は格子4,9のデータ，プロセッサ3は格子8,1(=13)のデータが，各時間ステップにおいて必要になります．

このようなプロセッサ間のデータの通信はMPIライブラリを用いて実装することになります．以下は，MPIライブラリを用いた並列化例です． （以下にサンプルソースコードが表示されない場合はこちらのサンプルコードを参照してください．）

MPIソースコードの変更点を見てみましょう．まず，第1にMPIによって並列化することを"宣言"しなければなりません．11行目のuse mpi．MPIモジュールによってMPIによって提供されるサブルーチンや変数が使用可能になります．MPIソースコードのうち並列化されている箇所はサブルーチンmpi_init, mpi_finalizeで囲まれ，それらの間で複数のプロセッサを使用することができます．並列化された箇所で，各プロセッサがまずするべきことは，自分のプロセッサ番号（ランク）［mpi_comm_rank］と全プロセッサ数［mpi_comm_size］を取得することです．プロセッサランクと全プロセッサ数から，59-66行目で自分が受け持つ格子点の範囲を計算します．$f$を計算する処理は，この範囲を用いて各プロセッサに分散されることになります．先に説明したように，各プロセッサは，必要なデータを取得するために両隣のプロセッサと通信する必要がありますが，この通信を行うサブルーチンがmpi_sendとmpi_recvです．サブルーチンmpi_gathervに関する部分は，データを出力するために全データを1つのプロセッサ上に集めるための処理です．逆に，mpi_bcastは1つのプロセッサが持っているデータを他の全てのプロセッサに一度に伝達するサブルーチンです．標準入力からの入力を1つのプロセッサだけが行い，読み込んだデータをmpi_bcastによって全プロセッサに送信する方法をとっています．

通信

1対1通信

mpi_send/mpi_recvによってデータ通信を行っている所が4ヶ所あります．周期境界条件のため両端のプロセッサがデータを送受信する所と，各プロセッサが右隣，左隣に受けもっているデータの境界のデータを送受信するシフト通信する所それぞれ2ヶ所づつです．それぞれMPIサブルーチンをコールする前に変数p_send/p_recvにデータを送受信するプロセッサランクを定義しています．最初のブロック（188-200行）では，プロセッサ0はf(NBX+1:NBX+NBX)を送信し，プロセッサnps-1はプロセッサ0からのデータを受け取りf(NX0+NBX+1:NX0+NBX+NBX)に保存します．他のプロセッサは何もしません．mpi_send/mpi_recv引数の送受信先プロセッサランクに"mpi_proc_null"を与えると，これらのサブルーチンは何もすることなく，ただちに返ります．

集団通信

mpi_gathervはデータを1つのプロセッサに集め，mpi_bcastはデータを全プロセッサに送信します．これらのサブルーチンはコミュニケータ（mpi_comm_world）で定義されたプロセッサのグループ（通常すべてのプロセッサ）間で集団的にデータ通信を行います．

データの入出力について

MPIプログラムでは，分割されたデータをどのように入出力するかについて検討する必要があります．入出力は1つのプロセッサに押しつけておく方法が簡単ですが，無用な通信が発生したり，取り扱うデータが大規模になる場合，そもそも単一のメモリ上に格納することが不可能になります．一方，各プロセッサが別々のファイルを用いて入出力を行う場合，プロセス数が多くなるとファイル数も増加し，ファイルの取り扱いが煩雑になります．複数プロセッサが同一のファイルに別個のデータを入出力する方法（並列I/O）も可能です．サンプルプログラムでは，簡単のために1つのプロセッサにデータを集めて出力を行うことにしました．

Fortranユーザへの注意

C言語版MPIライブラリでは，各サブルーチンは返り値としてエラーコードを返します．Fortranでは，サブルーチンは返り値を持ちませんので，エラーコードはサブルーチンの最後の引数として与えられます．よって，C言語版に比べてFortran版では，サブルーチンの引数が1つ多く必要で，最後に必ずエラーコードのための整数の引数を取ります．通常，エラーが生じるとプログラムはただちに異常終了しますので，このエラーコードを参照することはありません．

コミュニケータ

mpi_comm_worldとは，互いに通信するプロセッサのグループを含むコミュニケータのことです．タグのような意味で使われますが，通常コミュニケータを必要とする所ではmpi_comm_worldと書いておけば十分です．

デッドロック

周期境界条件のための通信を行っている箇所（188-200, 202-214行）は，シフト通信（216-227，229-240行）と，p_send/p_recvをうまく設定すればまとめることができそうです．222-223行目をp_recv=nps-1/p_send=0，235-236行目をp_send=nps-1/p_recv=0とすれば，188-214行目を取り除くことができます．しかし，このようなプログラムは，残念ながら，あるシステムにおいては上手く動作しません．mpi_sendはブロッキング通信を行うサブルーチンで，送信するデータをシステムバッファにコピーするまで返りません．図5上図に示すように，システムが十分大きなバッファを持つ場合，プログラムは正しく動作しますが，下図のようにバッファサイズが十分でない場合，mpi_sendは終了せず，プログラムはそれ以降に進めないことになります．このように，すべてのプロセッサが待ちの状態になってしますことを，"デッドロック"と言います．

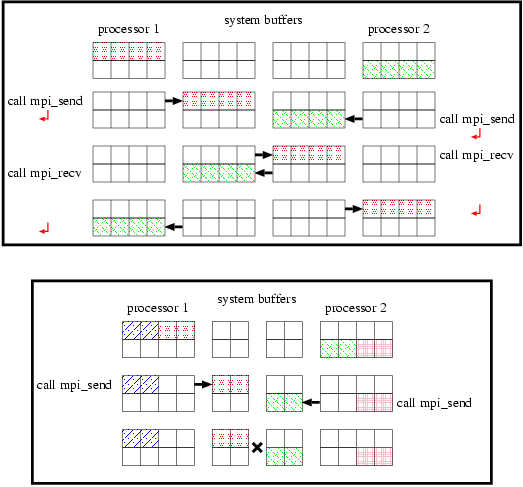
mpi_sendとmpi_recvの順序を入れ換えるとどうでしょうか？状況はさらにひどく，システムバッファのサイズに依存せず，全てのシステムで明らかにデッドロックとなります．なぜなら，mpi_recvもブロッキング通信を行うサブルーチンであり，受信するべきデータを受け取るまで返りませんので，すべてのプロセッサがmpi_recvをコールして時点でプログラムはストップします．

デッドロックを回避する方法がいくつかあります．送受信するプロセッサのうち一方がmpi_sendをコールし，他方がmpi_recvをコールする場合，システムバッファが十分でない場合でも通信は成功します（図6）．

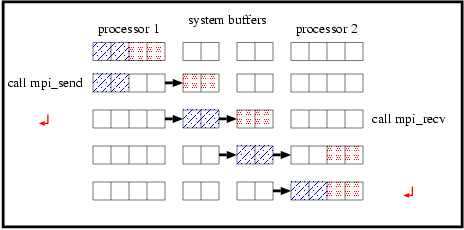
つまり，偶数/奇数番プロセッサがmpi_send/mpi_recvを先にコールするように変更すればよいことになります．または，これを自動的に行うmpi_sendrecvというサブルーチンも用意されています．

デッドロックを避ける他の方法として，非ブロッキング通信を行うサブルーチンを用いる方法があります．mpi_isendとmpi_irecvは非ブロッキング送受信を行うサブルーチンで，ただちに返ります．ブロッキング通信を行うサブルーチンを用いる理由は，それらがデータの正しさを保証してくれるためであり，逆に，非ブロッキング通信ではデータへの不正なアクセスを許してしまいます．これはmpi_irecvの挙動を見れば一目瞭然です．次のようにmpi_irecv(recvbuf,...)をコールし，直後で受け取るはずのデータrecvbufを参照するとしましょう．

	      call mpi_irecv(recvbuf,....)
tmp=recvbuf*recvbuf
	    

mpi_irecvがすでにrecvbufを受け取ったという保証はありませんので，recvbufには正しく値が代入されていないかもしれません．同様なことがmpi_isendにも起こり得ま す．mpi_isendの直後に送信すべきデータにアクセスすると，思いがけずそのデータを上書きしてしまうかもしれません．mpi_irecv/mpi_isendがデータを受信/送信するまで待つためのサブルーチンがmpi_waitです．非ブロッキング通信サブルーチンを用いて，送受信する部分を書き直すと以下の様になります．

	      call mpi_isend(sendbuf,...,ireq1,...)
call mpi_irecv(recvbuf,...,ireq2,...)
call mpi_wait(ireq1,...)
call mpi_wait(ireq2,...)
	    

	      total0=sum(f(npmin(pid):npmax(pid)))*dx
call mpi_reduce(total0,total,1,mpirealtype,mpi_sum,rootproc,mpi_comm_world,ierr)
	    

派生型

MPIプログラミングにおいて最も重要なことは，いかにデータ通信量を減らすかということです．MPIサブルーチンコールには時間がかかりますので，コールの回数を減らすことは効果的です．例にあげたソースコードでは55-57行目にあるmpi_bcastをひとつにまとめることができそうです．（実際には，この変更はまったく効果はありませんが，派生型の例を示すために取り上げています。）

MPIライブラリでは，送受信されるデータをグループ化する枠組が提供されています．派生型と呼ばれるデータのグループを表すデータ型をユーザが定義し，それを一般のMPIのデータ型と同様に用いることができます．派生型を定義するためには，グループ化する各要素のデータ型，位置および大きさ（配列のサイズ）が必要になります．図7にデータのグループの例を示します．

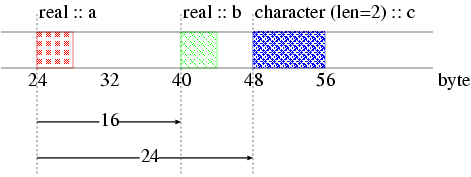
図7の例では，データグループは，2つのreal型（a, b）および長さが2のcharacter型（c）で構成されています．各要素の位置は，1番目の要素（a）からの変位で表されますので，a, b, cの位置は，それぞれ0, 16, 24ということになります．

以下のサブルーチンで，サンプルプログラムで用いられる派生型（newtype）を定義します．

	      subroutine inputtype(int1,int2,int3,newtype)

  use mpi

  implicit none

  integer, intent(in) :: int1,int2,int3
  integer, intent(out) :: newtype
  integer, parameter :: count=3
  integer :: i
  integer (kind=mpi_address_kind) :: addr_start
  integer :: blen(count)
  integer (kind=mpi_address_kind) :: disp(count)
  integer :: tlst(count)

  integer :: ierr

  blen=(/ 1,1,1 /)

  tlst=(/ mpi_integer,mpi_integer,mpi_integer /)

  call mpi_get_address(int1,disp(1),ierr)
  call mpi_get_address(int2,disp(2),ierr)
  call mpi_get_address(int3,disp(3),ierr)
  addr_start=disp(1)
  do i=1,count
     disp(i)=disp(i)-addr_start
  end do

  call mpi_type_create_struct(count,blen,disp,tlst,newtype,ierr)
  call mpi_type_commit(newtype,ierr)

  return

end subroutine inputtype
	    

データのグループは3つの要素（int1=NX0, int2=NT, int3=NOUT）で構成され，それぞれの位置，データ型，大きさは配列blen，tlst，dispに代入されています．mpi_get_addressはデータの位置を与えます．与えられた情報をもとに，mpi_type_create_structが新しい派生型（newtype）を構築し，その新しい派生型はmpi_type_commitによりMPIに通知されたあとに使用可能になります．作成された新しい派生型を用いて，1回mpi_bcastを呼ぶことでデータのブロック（NX0, NT, NOUT）を送信するには以下のように変更すればよいことになります．

	      call mpi_bcast(nx0,1,intype,rootproc,mpi_comm_world,ierr)
	    

この操作でNX0だけでなく，（NX0, NT, NOUT）が送信されます．

ソースコードなどのセット

Subversionリポジトリから，public→tutorials→diffuseを辿りダウンロードしてください．

	      make
	    

	      make MPI=16